Diese Seite funktioniert nur mit Javascript.
Präferenzen und Nutzenfunktion2.2.2 Der GrenznutzenGrenznutzen und Unsicherheit
Nun haben wir gerade gesehen, dass man den Zahlenwert, den eine Nutzenfunktion liefert, nicht als Nutzeneinheiten interpretieren kann, trotzdem gehen wir in diesem Abschnitt genau davon aus. Dafür gibt es zwei Rechtfertigungen. Erstens hat sich die mikroökonomische Theorie historisch so entwickelt. Zweitens lässt sich mit dieser Annahme die Nachfragefunktion nach einem Gut sehr einfach ableiten. Zudem muss man auch heute noch auf die Annahme kardinal messbaren Nutzens zurückgreifen, wenn man Entscheidungsverhalten unter Unsicherheit analysieren will, wenn also Ereignisse nicht mit Sicherheit, sondern - wie z.B. in Lotterien - nur mit einer bestimmten Wahrscheinlichkeit eintreten.
Zunächst nehmen wir an, man könne das Wohlbefinden (den Nutzen) von Menschen in der Einheit Util ähnlich wie Fieber mit einem Thermometer messen. Der Maßstab sei dabei wie folgt festgelegt: Wenn man um einen Euro reicher wird, dann steigt der Nutzen um ein Util. Wenn man zehn Euro verliert, dann sinkt der Nutzen um zehn Utile usw.
Nun befragen wir einen Probanden, dem wir das Messkonzept erklärt haben, wie sich sein in Utilen gemessener Nutzen an einem bestimmten Abend in Abhängigkeit des Bierkonsums gestaltet. Das Bier messen wir dabei in kleinen 0,2-Liter-Gläsern. Die Situation, in der der Proband kein Bier trinkt, wird auf 0 Utile normiert. Die Frage, die an den Probanden gerichtet wird, lautet: "Stellen Sie sich vor, Sie würden x Biere trinken, wie hoch ist Ihr Wohlbefinden in Utilen?" Die Antworten auf die für unterschiedliche Mengen an Bier wiederholte Frage sind in der folgenden Tabelle wiedergegeben:
| Zahl der Biere
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Utile, Befragung
|
0
|
3
|
5
|
7
|
8
|
9
|
7
|
7
|
-
|
-
|
4
|
| Funktionswerte U
|
0,00
|
2,75
|
5,00
|
6,75
|
8,00
|
8,75
|
9,00
|
8,75
|
8,00
|
6,75
|
5,00
|
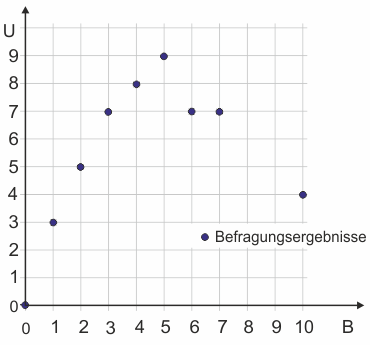
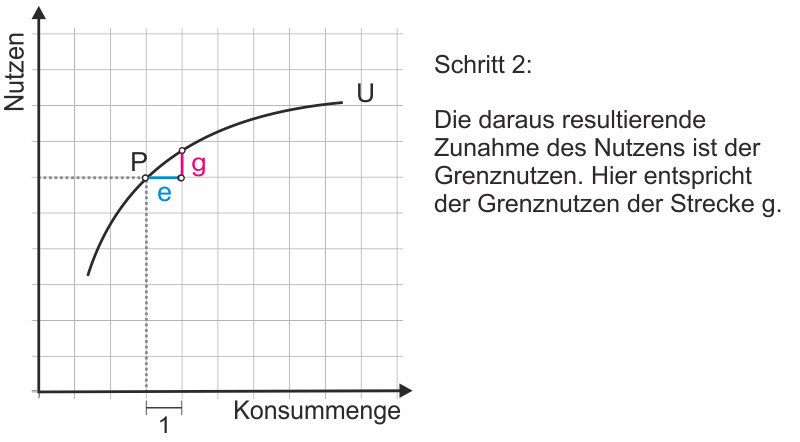
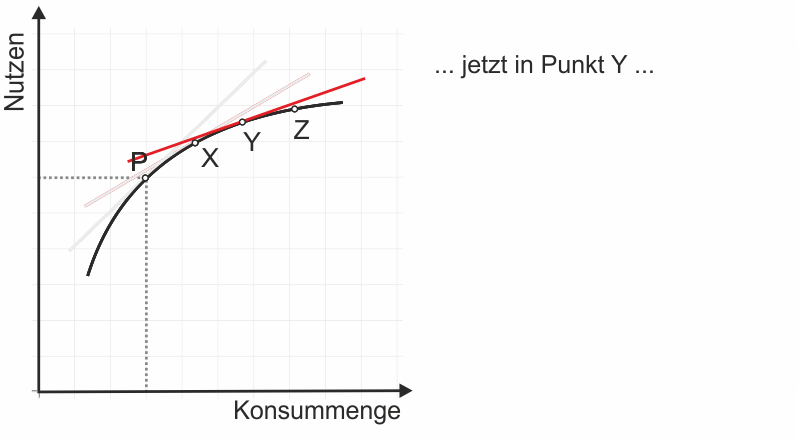
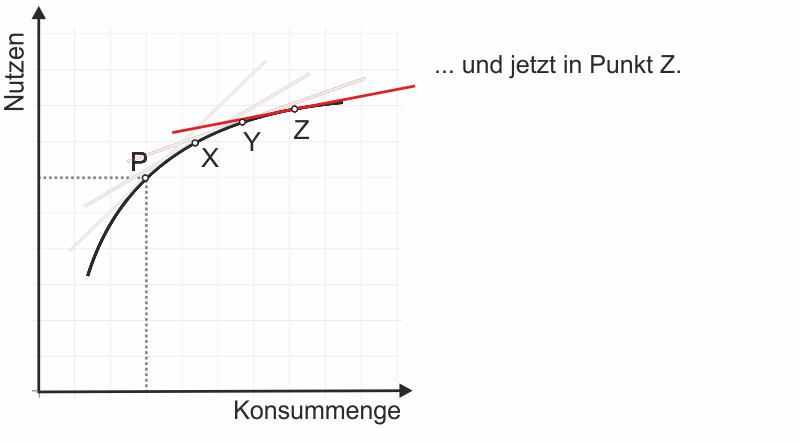
Wir können Tabelle 1 entnehmen, dass der Proband den größten Nutzen mit 5 Bieren erreichen würde. Wenn er sich also eine der Situationen aussuchen könnte, würde er sich für 5 Biere entscheiden - für die Situation, die ihm nach eigenem Bekunden den größten Nutzen stiftet. Die Fragen nach 8 und 9 Bier hat der Proband nicht beantwortet; die Regelmäßigkeit, die in seinen Antworten zu erkennen ist, lässt aber vermuten, dass sein Nutzen hier zwischen 7 und 4 Utilen liegen würde. Diese Regelmäßigkeit wird besonders deutlich, wenn man den Zusammenhang zwischen der Zahl an Bieren und den Utilen in ein Diagramm überträgt.
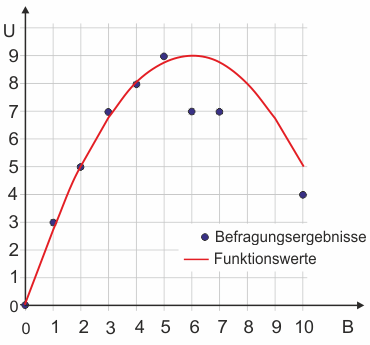
Es zeigt sich nahezu eine funktionale Abhängigkeit. Besonders im Bereich von 0 bis 5 Bieren lassen sich die Antworten des Probanden bis auf geringe Abweichungen mit der Funktion
$$U = 3B-0,25B^2 \tag{1}$$abbilden. $U$ steht in dieser Funktion für Utile, $B$ für die Zahl der Biere. Auch diese Funktion nennen wir Nutzenfunktion.
Besäßen wir als Information nur die Nutzenfunktion, würden wir eine leicht abweichende Prognose über das Verhalten des Probanden abgeben. Mit der Hypothese, dass der Proband die Menge Bier konsumieren wird, die seinen Nutzen (sein Wohlbefinden) maximiert, würden wir als optimalen Bierkonsum 6 Gläser ermitteln (da die Funktion für $B* = 6$ ein Maximum zeigt, wie man aus der Grafik unschwer erkennen, aber auch leicht nachrechnen kann).
Das nutzenmaximierende Verhalten des Probanden kann auch wie folgt beschrieben werden: Er dehnt den Bierkonsum aus, so lange der Nutzenzuwachs durch ein weiteres Bier positiv ist (s. Tab. 2).
| Zahl der Biere |
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Utile |
0
|
3
|
5
|
7
|
8
|
9
|
7
|
7
|
-
|
-
|
4
|
| Nutzenzuwachs in Utilen |
-
|
3
|
2
|
2
|
1
|
1
|
-2
|
0
|
-
|
-
|
-
|
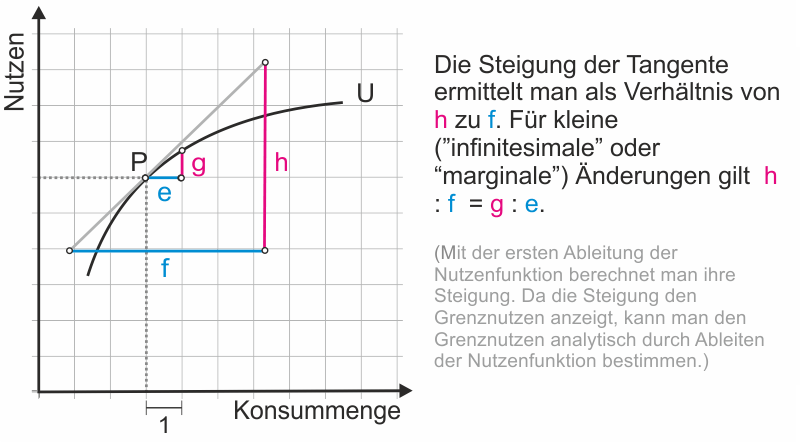
Für den in Tabelle 2 aus den Befragungswerten berechneten Grenznutzen - um wie viel steigt der Nutzen mit einem weiteren Bier? - finden wir eine gute Näherung mit der ersten Ableitungder Nutzenfunktion:
$${{{\rm{d}}U} \over {{\rm{d}}B}} = 3 - 0,5 \cdot B \tag{2}$$|
Zahl der Biere
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Utile
|
0
|
3
|
5
|
7
|
8
|
9
|
7
|
7
|
-
|
-
|
4
|
|
Nutzenzuwachs in Utilen
(Grenznutzen) |
--
|
3
|
2
|
2
|
1
|
1
|
-2
|
0
|
-
|
-
|
-
|
|
Wert der 1. Ableitung der Nutzenfunktion (2)
|
3,0
|
2,5
|
2,0
|
1,5
|
1,0
|
0,5
|
0
|
-0,5
|
-1
|
-1,5
|
-2,0
|
Die Werte der ersten Ableitung der Nutzenfunktion stimmen nur ungefähr mit den Nutzenzuwachswerten aus den Befragungsergebnissen überein, aber es reicht doch aus, um zu erkennen, dass die Steigung der Nutzenfunktion den Grenznutzen anzeigt. Solange die Steigung positiv ist, dehnt der Proband den Bierkonsum aus. Er erreicht den maximalen Nutzen, wenn die Steigung der Nutzenfunktion gleich Null ist. Das ist nichts anderes als die notwendige Bedingung für ein Maximum der Nutzenfunktion, nur in ungewohnten Begriffen: der Grenznutzen muss gleich null sein. Das ist bei 6 Gläsern Bier der Fall:
$$3 - 0,5B = 0\,\,\,\,\,\, \to \,\,\,\,\,\,B^* = 6 \tag{3}$$"Die Größe ein und desselben Genusses nimmt, wenn wir mit der Bereitung des Genusses ununterbrochen fortfahren, fortwährend ab, bis zuletzt Sättigung eintritt."
H. H. Gossen, 1854
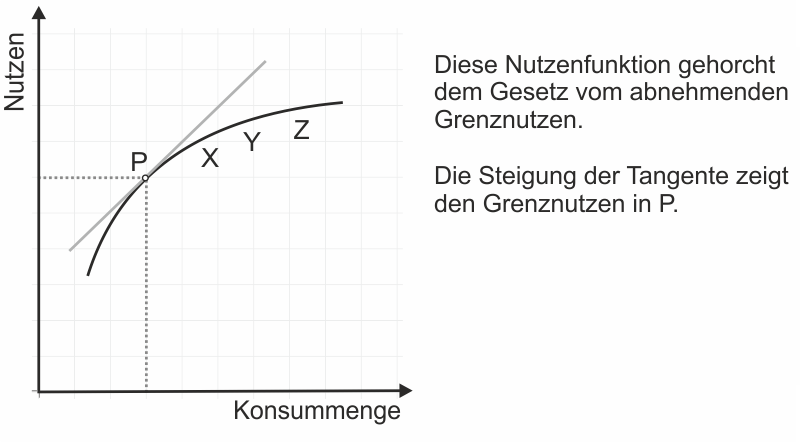
Bei der Betrachtung des Grenznutzens - unabhängig davon, ob aus den Antwortwerten oder der Nutzenfunktion berechnet - fällt auf, dass der Grenznutzen mit steigendem Bierkonsum abnimmt. Dazu hat Hermann Heinrich Gossen 1854 folgendes festgestellt (s. Kasten):
Diese Aussage ist als Erstes Gossensches Gesetz oder Gesetz vom abnehmenden Grenznutzen bekannt. Offenbar führt es in unserem Beispiel dazu, dass der Proband mit 6 Bieren genug hat, denn da "tritt bei ihm Sättigung ein". Gossen war der Meinung, dass das tägliche Leben für dieses Gesetz tausendfältige Tatsachen als Beweise liefere.
Da die Nutzenfunktion die Antworten des Probanden einigermaßen abbildet, werden wir im Folgenden die Originalwerte außer Acht lassen. Wir wollen nun annehmen, dass jedes Bier 2,00 Euro kostet, und überlegen, wie der Proband darauf mit seinem Bierkonsum reagieren wird. Dazu nehmen wir - zugegebenermaßen etwas gewagt - an, dass man den Nutzen aus Biertrinken und den Nutzen aus Geldbesitz einfach addieren darf, um zum Gesamtnutzen zu kommen. Die Nutzenfunktion des Biertrinkers soll nun also lauten
$${\rm{Gesamtnutzen = }}{U_{ges}}{\rm{ = Biernutzen + Geldnutzen = }}{U_B}{\rm{ }} + {U_G} \tag{4}$$Da annahmegemäß ein Euro einem Util entspricht (für das Gut Geld wird also von einem konstanten Grenznutzen ausgegangen), können wir mit $\bar G$ als Anfangsgeldbestand schreiben
$$U = \left( {3B - 0,25{\rm{ }}{B^2}} \right) + \left( {\bar G{\rm{ }} - {\rm{ }}2B} \right) \tag{5}$$Dabei zeigt der erste Klammerterm den Nutzen aus Bierkonsum und der zweite Klammerterm den Nutzen aus Geld. Außerdem ist berücksichtigt, dass sich der Geldbestand mit jedem Bier B um 2,00 Euro vermindert.
Nun bereitet es keine Schwierigkeiten, die notwendige Bedingung für ein Nutzenmaximum zu berechnen (da es sich bei der Nutzenfunktion offensichtlich um eine nach unten geöffnete Parabel handelt, schenken wir uns die Überprüfung der hinreichenden Bedingung für ein Maximum):
$${{dU} \over {dB}} = 3 - 0,5 \cdot B - 2\mathop = \limits^! 0 \tag{6}$$ $${B^*} = 2 \tag{7}$$Das Ergebnis ist nicht unplausibel: während der Proband 6 Gläser Bier trinken würde, wenn er sie kostenlos bekäme, fragt er zum Preis von 2,00 Euro pro Glas nur noch 2 Bier nach.
Auf die gleiche Art und Weise können wie ermitteln, wie viele Biere $B$ der Proband zu einem beliebigen Preis $p$ pro Glas nachfragen wird:
$$U = (3B - 0,25{B^2}) + (\bar G - p \cdot B) \tag{8}$$ $${{{\rm{d}}U} \over {{\rm{d}}B}} = 3 - 0,5 \cdot B - p\mathop = \limits^! 0 \tag{9}$$ $${B^*} = 6 - 2p \tag{10}$$Dieser Zusammenhang zwischen der nutzenmaximierenden Biernachfrage und dem Bierpreis ist die Nachfragefunktion des Probanden für Bier.
Der negative Zusammenhang zwischen Bierpreis und nachgefragter Biermenge ist darauf zurückzuführen, dass für den Bierkonsum des Probanden das Gesetz vom abnehmenden Grenznutzen gilt. Das wollen wir uns am Beispiel eines Bierpreises von 1,00 Euro noch einmal klar machen:
Zunächst berechnen wir mit der Nachfragefunktion (10) für einen Preis von 1,00 Euro eine optimale Biernachfrage von 4 Gläsern. Jedes Bier, das der Proband trinkt, sorgt für einen Nutzenentgang ("Disnutzen") von 1 Util, denn jedes Bier kostet 1,00 Euro und die entspricht annahmegemäß einem Util. Der Grenznutzen des ersten Bieres beträgt 2,5 Utile (s. Tab. 3). Damit liegt der Nutzenzuwachs aus dem Bierkonsum über dem Nutzenentgang aus der Geldausgabe. Also wird das erste Bier getrunken. Der Grenznutzen des zweiten Bieres beträgt 2 Utile. Also wird auch das zweite Bier getrunken. Der Grenznutzen des dritten Bieres beträgt 1,5 Utile. Also wird auch das dritte Bier getrunken. Der Grenznutzen des 4. Bieres beträgt 1 Util. Es wird gerade noch getrunken. Der Grenznutzen des 5. Bieres wäre nur noch 0,5 Utile. Dafür gibt der Proband keinen Euro mehr her, denn dann würde er ein Util aus- bzw. aufgeben, um ein halbes Util zu bekommen.
Warum eigentlich sind Diamanten so teuer, obwohl sie nur einen geringen Gebrauchswert besitzen? Und warum ist Wasser so günstig, wo es doch so einen hohen Gebrauchswert hat? Kurz: Wie kann es sein, dass Gebrauchs- und Tauschwerte von Gütern so weit auseinander liegen?
Auf dieses unter dem Namen Wertparadox bekannte Problem liefert das Gesetz vom abnehmenden Grenznutzen die folgende Antwort:
Aus dem Biertrinker-Beispiel ist bekannt, dass der Konsum ausgedehnt wird, bis der Grenznutzen mit dem Preis übereinstimmt. Ein Blick in Tabelle 3 zeigt, dass die erste Ableitung der Nutzenfunktion (=Grenznutzen) für zwei Biere den Wert 2 annimmt. Liegt der Bierpreis bei 2 Euro werden aber gerade auch 2 Bier nachgefragt. Bei einem Bierpreis von 1 Euro werden 4 Biere nachgefragt und auch in diesem Fall stimmt der Preis wieder mit dem Grenznutzen überein. Für jede nach Gleichung (10) gleichgewichtige Biernachfrage lässt sich leicht überprüfen, dass der zugehörige Preis jeweils mit dem Grenznutzen übereinstimmt.
An dieser Stelle sei noch einmal betont, dass der Preis ein Datum ist. Stimmen Preis und Grenznutzen nicht überein, kann der Konsument seinen Nutzen durch eine Veränderung der Konsummenge erhöhen, da sich mit ihr die Höhe des Grenznutzens verändert. Liegt der Grenznutzen z. B. über dem Preis, dann dehnt der Konsument den Konsum aus. Die gestiegene Menge lässt - vorausgesetzt das erste Gossensche Gesetz trifft zu - den Grenznutzen sinken, sodass es zu einer Annäherung von Grenznutzen und Preis kommt.
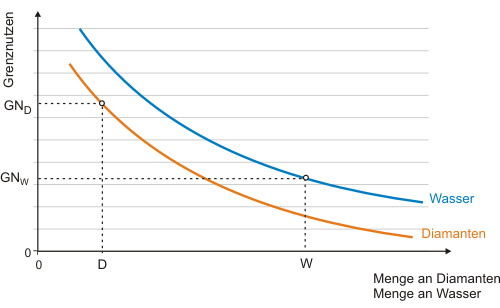
Zurück zum Wertparadox: Die nachstehende Abbildung zeigt für gleiche Mengen Wasser und Diamanten (beide Güter könnten z. B. in kg gemessen werden) jeweils einen höheren Grenznutzen für Wasser. Mit der Feststellung, dass Preis und Grenznutzen übereinstimmen, würde das bei einem gleich hohen Bestand von Wasser und Diamanten einen höheren Preis für ("das nützlichere Gut") Wasser bedeuten.
Für beide Güter ist die Gültigkeit des ersten Gossenschen Gesetzes angenommen, wie man aus dem Verlauf der Grenznutzenfunktionen unmittelbar erkennen kann. Bei einem hohen Bestand an Wasser W ist demzufolge mit einem geringen Grenznutzen GNW zu rechnen. Hingegen führt die Knappheit der Diamanten (Menge D) zu einem hohen Grenznutzen GND.
Welche dieser Verwendungen würden die Haushalte zuerst einschränken oder einstellen, wenn der Preis für Wasser ansteigen würde? Sind dies bei allen Haushalten die gleichen Verwendungen?
Das Paradox löst sich also auf. Ohne Frage gibt ein Verdurstender in der Wüste 1 kg Diamanten für einen Liter Wasser. Für ihn, für den beide Güter gleich knapp sind, ist der Grenznutzen des Wassers höher. (Achten Sie einmal darauf, wie manche Filme ihre Spannung dadurch gewinnen, dass vermeintlich freie Güter wie Luft oder Wasser, aber z. B. auch Zugang zu Informationen, sehr knapp und damit nahezu unbezahlbar werden.) Die Bundesbürger hingegen sprengen damit ihren Rasen, waschen ihr Auto oder füllen ihren Swimmingpool. Ihr Verhalten ist dennoch rational, denn der niedrige Wasserpreis leitet das Wasser in Verwendungen, die den Grenznutzen auf eben diese Höhe drücken.
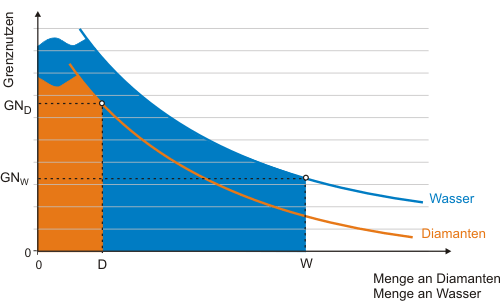
Der gesamte in der Abbildung durch die Menge an Wasser W erzeugte Nutzen ist größer als der Gesamtnutzen der Diamantenmenge D. Dies wird in der Abbildung gezeigt, wenn der der Mauszeiger über das Diagramm gestellt wird. Da die Grenznutzenkurven die Ableitungen der Nutzenfunktionen sind, entsprechen die Flächen unter den Grenznutzenkurven den jeweiligen Gesamtnutzen.
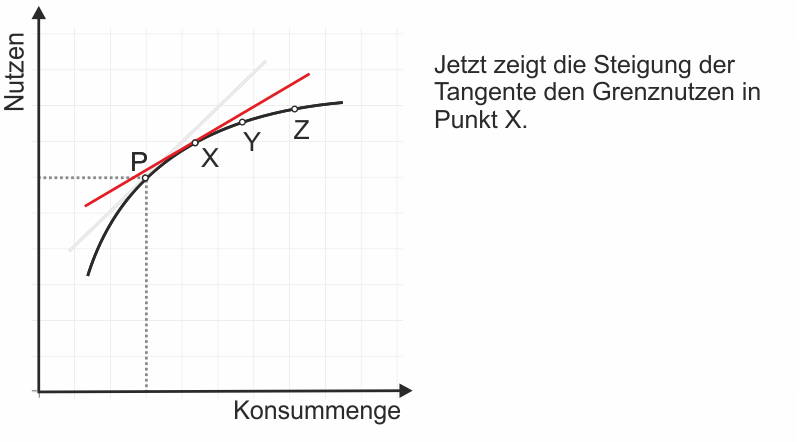
Grafisch kommt der Grenznutzen in der Steigung der Nutzenfunktion zum Ausdruck, analytisch lässt sich der Grenznutzen über deren erste Ableitung ermitteln (s. Gleichung (2)). Wenn die Steigung abnimmt, gilt das erste Gossensche Gesetz. Analytisch muss demnach die Steigung der ersten Ableitung untersucht werden. Die Steigung der ersten Ableitung wird über die zweite Ableitung bestimmt (das ist die erste Ableitung der ersten Ableitung).
Im Zahlenbeispiel findet man für die zweite Ableitung
$${{{\rm{d}}{{\kern 1pt} ^2}U} \over {{\kern 1pt} {\rm{d}}{B^{\rm{2}}}}} = - 0,5 \tag{1}$$Unabhängig von der Höhe des Bierkonsums nimmt der Grenznutzen mit jedem weiteren Bier also um 0,5 Einheiten ab. Es handelt sich dabei um jenen Wert, den man in der untersten Zeile von Tabelle 3 durch die Differenzenbildung je zwei benachbarter Werte errechnet.
Würde man für die zweite Ableitung der Nutzenfunktion einen Wert von null errechnen, wäre der Grenznutzen konstant. Das erste Gossensche Gesetz träfe dann nicht zu. Ein konstanter Grenznutzen wird oft (wie auch hier) für Geld angenommen. In fortgeschrittenen Analysen lässt sich darüber hinaus modellieren, ob ein Wirtschaftssubjekt risikofreudig (zunehmender), risikoneutral (konstanter) oder risikoavers (abnehmender Grenznutzen des Geldes) ist.
Natürlich gilt das erste Gossensche Gesetz erst recht nicht, wenn sich ein positiver Wert für die zweite Ableitung der Nutzenfunktion ergibt. Mit etwas gutem Willen könnte man ein solches Ergebnis als Sucht interpretieren: das zweite Bier bringt mehr Nutzen als das erste, das dritte mehr als das zweite, das vierte mehr als das dritte ... Der Biertrinker würde seinen Konsum also ausdehnen, bis irgendwelche Restriktionen greifen, die im Modell bisher nicht berücksichtigt sind.
Nach ähnlichen Seiten im WWW suchen